How can we… use AI to support clinical decision-making in intensive care?
19 February 2026
Challenger Mishra and Subhayan Roy Moulik
24 October 2022
Machine learning
The innate ability of quantum computers to simulate quantum mechanics opens up new paradigms for computation that were largely unimagined before, and could pave the way for exciting new breakthroughs. Searching for problems that are intractable for a classical computer, but which a quantum device can solve, is an active area of research. Although such a problem need not necessarily have a scientific rendition, utilising quantum computing to achieve breakthroughs in scientific problems could pave a way for demonstrating quantum supremacy itself.
Machine learning has led to major breakthroughs in a myriad of scientific endeavours, such as drug design and discovery, determining outcomes of chemical reactions, catalyst design, and determining structures of proteins. However, it has played a more modest role in advancing mathematics, or mathematically intensive scientific disciplines. Recently, there has been an explosion of interest in utilising machine learning in studying various aspects of geometry, topology, knot theory, and representation theory. Theoretical Physics, and often String theory (which is a theory of quantum gravity), has been hugely influential in driving many such developments, either through percolation of ideas, or by providing an effective testbed for machine learning and quantum computing. Recent developments in machine driven studies of algebraic geometry of complex Calabi—Yau geometries (which appear as extra-dimensions in certain String theories), is a pertinent example.
One grand ambition is to simulate quantum field theories such as quantum electrodynamics and the Standard Model on quantum computers to make predictions about experiments and infer fundamental properties of quantum mechanical systems. Mathematicians and physicists could compare numerical predictions with experimental data collected from the Large Hadron Collider, for example, to find anomalies and test theories accurately with high computational efficiency. It was recently shown that it is possible to utilise machine learning to accurately infer masses of particles (such as protons, neutrons, pentaquarks, etc) from knowledge of their quantum numbers. This bypasses the computationally expensive machinery of (Lattice) Quantum Chromodynamics — the theory of quarks and gluons. Additionally, it was shown that machine learning could help test hypotheses surrounding compositions of composite particles which have been experimentally detected but theoretically not fully understood. Quantum computing in the near term would add tremendous value in addressing some of the computational bottlenecks in problems afforded by String phenomenology — the paradigm connecting string theory to our four dimensional observable universe. This would likely shed more light into underlying the mathematics that is fundamental to constructions in theoretical physics, particularly string theory.
Using new tools to answer questions in String Theory
There are a plethora of unanswered questions coming from theoretical physics and string theory (which hypothesises that matter is fundamentally made out of vibrating string-like objects) that machine learning could help unlock. Although classical computers have had considerable success in addressing such questions in a deterministic sense, a number of questions still remain intractable. As such, there is a growing attempt to reformulate problems in the language of machine learning and quantum circuits. This process itself is experimental, because while there is little doubt that quantum computers are powerful tools for research, what they are good at is not so certain. Similarly, although machine learning has been impactful across a number of scientific endeavours, advancements have often occurred at the cost of interpretability. This is primarily due to the lack of a mathematically grounded understanding of deep learning. Frameworks for ‘Quantum Machine Learning’ which brings the formalism of quantum mechanics to machine learning is likely to shed light into the theory of deep learning itself. At present it is being successfully deployed in applications ranging from image classification to anomaly detection.
We are employing machine learning to gain insights into problems in theoretical physics and to further our understanding of how quantum computers could be deployed in this sector. One of our overlapping interests involves the study of geometries that feature as extra- dimensions in string theory. In certain string theoretic settings, these extra-dimensions appear as complex geometries called Calabi—Yau manifolds. Named after Eugenio Calabi and Shing-Tung Yau, these geometries have proven to be fundamental not only in understanding string theory as a theory of our universe, but also in exposing connections between seemingly disjoint fields of mathematics. Mirror symmetry is a fascinating example of this phenomenon. This two-fold symmetry is best represented by the ‘Hodge plot’ [Figure 1].
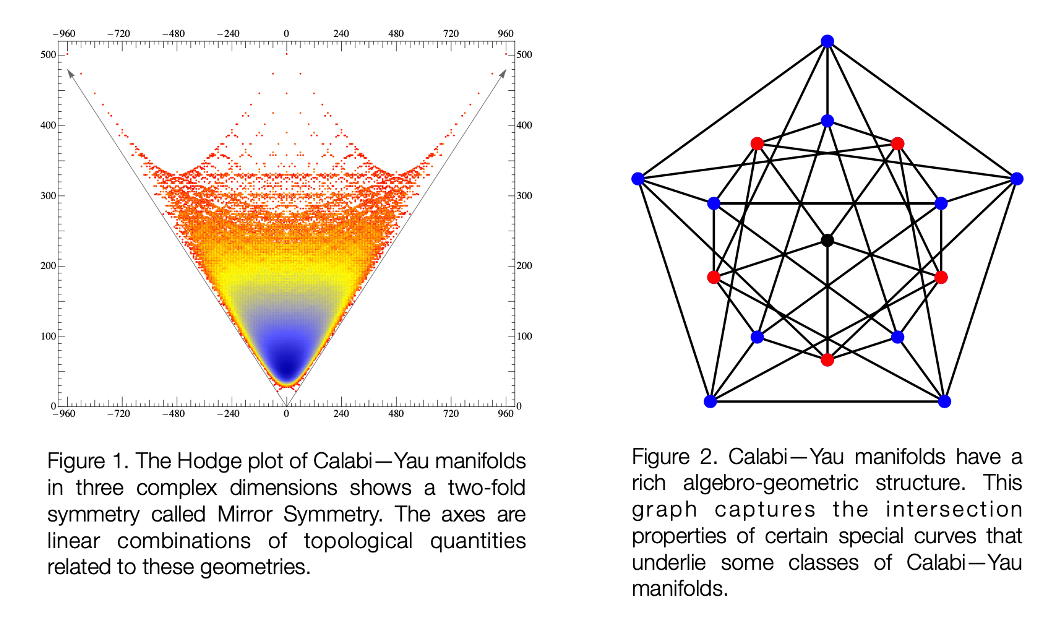
Calabi–Yau manifolds have a rich algebraic and geometric structure [Figure 2]. Einstein’s for which the fiber is a K3 manifold. Different types of K3 fibers give rise to distinct webs. Along theory of general relativity posits an intricate connection between gravity and the curvature of spacetime. The formalism is however agnostic to the number of dimensions of space. General relativity gives a description of a quantity called a metric, which is a distance function on a given spacetime geometry. In string theory, spacetime is often understood as having two components — the ordinary four dimensional spacetime (M) and the postulated extra-dimensions of space, represented by Calabi—Yau geometries (Y). Thus spacetime in this context is expressed as M x Y. One problem of interest is to find a metric that spans the both the ordinary and extra-dimensional space, that is consistent with Einstein’s equations in vacuum. These equations are typically a coupled set of non-linear partial differential equations which are in general hard to solve analytically especially in setting of complex geometries.
In the late 1970s, Calabi conjectured that such a metric exists and Yau proved its existence to win the Fields Medal in 1982. Since then, mathematicians and physicists have failed to arrive at an analytic form for this distance function on the Calabi-Yau manifold in the relevant number of dimensions, although substantial progress was made in understanding this problem in an approximate sense. There are various formulations of this problem — Donaldson’s algorithm and Ricci flow being two prominent ones. Such approaches would likely benefit from a machine learning or a quantum computing approach. Machine learning was recently utilised to find an approximate solution to the problem of finding metrics consistent with Einstein’s equations. One problem of mutual interest is in designing an efficient quantum circuit to find a metric over Calabi—Yau manifolds in three dimensions that satisfies Einstein’s equations in vacuum.
Joined-up thinking
We are now beginning to better understand how to utilise the computational prowess of quantum computers and machine learning methods to tackle questions arising in theoretical physics. For example, we observed that an application of quantum computers to speed up search problems (using a textbook algorithm called Grover’s search) can have consequential bearings for the problem of determining new solutions to string field equations. This will help build ever more realistic string theoretic models of our universe whilst shedding light on the underlying algebraic-geometry of such constructions.
Current quantum computers are at their nascent stage of development, and implementing and designing quantum algorithms remains extremely challenging. However, our modest findings have encouraged us to imagine how we might better use quantum computing as a resource for scientific discovery. To this purpose, the Computer Laboratory recently hosted Subhayan for eight lectures aimed at computer scientists and researchers called ‘Quantum Algorithms for X’ to outline the machinery of quantum circuits and how they can be used to solve scientific problems.
The central purpose of the lectures was to give the participating researchers a self-contained introduction to the foundational tools used widely to develop quantum algorithms, so that they can independently access the usefulness of the quantum machinery, and build their own quantum algorithms to tackle the interesting problems they are trying to solve. We hope the programme will allow people to share knowledge and lead to collaborative efforts, as quantum machine learning is a developing area of research. We see this as a long-term venture and anticipate that while initially progress will be slow, it will eventually accelerate scientific discovery.
The future of problem solving
In the near-term, machine learning and quantum computing could be used to prove certain types of theorems that suit quantum architecture. In the longer term, we believe the rise of better machine learning and AI will inform the ways we do science, and quantum computing could help facilitate breakthroughs related to drug discovery, nitrogen fixation, data analysis and more.
We are exploring the potential of simulating particle physics and dynamics in particular using quantum machines with the aim of better understanding the chaotic properties of black holes, and expect many other mathematical discoveries to be born out of this technology. There’s a whole universe of potential.